The acoustic performance of selected precipitation hardened stainless steels and heat-treated titanium under substantial dynamic stress at ultrasonic frequencies.
David Wuchinich
Modal Mechanics
Yonkers, NY
Copyright David Wuchinich 2002
Abstract:
The mechanical Q of heat-treated
6Al-4V titanium and the recently developed high strength precipitation hardened
stainless steels, Custom 455 and Aermet 100, is measured in slender specimens
at cyclic stresses up to 200 MPa (30,000 psi) at a frequency of 20 kHz. The
results reveal that although these materials have impressive S/N
characteristics and very high yield strengths their use in making high
intensity ultrasonic resonators is severely limited by concomitant acoustic
loss.
Introduction
The author and others have
reported measurements of the mechanical Q obtained from chiming right circular
bars of various materials[1]. The technique, however, subjects the
materials to dynamic strains at most one tenth those of practical interest in
high intensity ultrasonic horn design and, moreover, does so at frequencies
again about one tenth those encountered in ultrasonic operation. Typically, and depending upon the material,
ultrasonic horns vibrate at peak dynamic strains between 0.025 and 0.25
percent. Mason has shown that in many
materials the elastic loss increases with strain[2]. Measurements made at very low strains may
not then provide accurate predictions of the loss encountered in horns designed
for practical applications.
Using mass-spring-mass resonators
that subject the material to nearly constant strain, Mason evaluated the
acoustic Q of the alloy 6Al-4V titanium at 17 kHz and found that the Q of
20,000 remained approximately constant for strains up to 0.25 percent,
thereafter decreasing dramatically[3]
and Puskar[4]
later found the Q of low carbon steel to be about 250 for strains up to 0.01
percent, decreasing to values in neighborhood of 100 as strains of 0.1 percent
were approached. However, within the
last decade very high strength stainless steels have been produced which
exhibit, after appropriate heat-treating, very low elastic losses at values of
strain below 0.01 percent and exceptional fatigue characteristics when
evaluated at high reversed strains using low frequency dynamic bending test
equipment[5].
It is known that the 316 stainless
steel alloy can withstand indefinitely strains of about 0.03 percent at
frequencies in the vicinity of 20 kHz and that the annealed titanium alloy,
6Al-4V, at the same frequencies can endure strains of 0.25 percent. Such performance, for example, enables the
design of titanium prismatic extensional resonators having free face excursions
of as much as 150 microns (0.006 inches) at 20 kHz and permits the design of
slender tapered extensional resonators with output displacements of 300 or more
microns. But two of the new stainless
steel alloys, Carpenter Custom 455 and Carpenter Aermet 100 have demonstrated
indefinite survival at 0.25 and 0.5 percent, respectively, in dynamic tests
conducted in the range of several to several hundred hertz[6]. If this behavior is preserved at ultrasonic
frequencies, the performance of titanium in producing the largest ultrasonic
displacements available is equaled, in one case, and exceeded by the other. In addition, 6Al-4V titanium, heat treated
for high strength, exhibits an 40 percent increase in static strength[7]. If this improvement is preserved under
dynamic conditions at ultrasonic frequencies, a substantial increase in the
free face excursion of heat treated resonators may result.
Method
Although Mason, Kuz’menko and Puskar utilized specially machined resonators which provided almost uniform strain, it is possible to use simple prismatic samples cut from raw stock to measure vibrational loss if the loss itself is not dependent upon strain.
All specimens evaluated were in the commonly provided shape of rolled or ground round rods. Using a 20 kHz piezo-electric transducer capable of supplying up to 500 watts of acoustic power, equipped with a titanium velocity transformer capable of providing up to a 150 micron at its free face, the rods were cut to a length that, when attached to the velocity transformer, produced a resonant frequency of approximately 20 kHz. All specimens measured approximately 12 mm (0.5 in.) in diameter and 130 mm (5 in.) in length. The connection was made by drilling and tapping one face of the rod and threading onto the velocity transformer using a floating threaded stud. In the absence of a test specimen connection, a short titanium cap having a integral thread was attached to the booster.
The Custom 455 specimen was heated
to 900 F and allowed to air cool, providing properties known as the H900
condition. In this state the material
is specified to have a yield strength of approximately 1700 Mpa (245 kpsi). The hardness is specified as well as
Rockwell C50.
The Aermet 100 specimen was first
heated to 1650 F for one hour, allowed to air cool, then refrigerated at –100 F
for one hour, allowed to air cool and finally soaked at 875 F for four hours,
followed by air cooling. This schedule
is specified to produce a state in the material with approximately the same
yield strength as the treated Custom 455.
Heat treated, Aermet 100 has a Rockwell C hardness of about 55.
The titanium sample was heated to
1725 F for one hour and then water quenched.
In this condition the yield strength is specified to be 1200 Mpa (170
kpsi). The material has a Rockwell C
hardness of 65.
To avoid complication of power
dissipation in an inductor that is commonly used to compensate for the inherent
capacity of piezo-electric ceramics employed, the transducer was directly
driven from a sinusoidal voltage source whose frequency and amplitude was adjustable. In the absence of tuning power delivery to
the transducer contains a large reactive component which, when much larger than
the real power consumption, may make measurements uncertain. The energy consumption of the transducer was
therefore measured using an oscilloscope technique in which the time integral
of the driving current or alternatively, driving voltage, and a signal
proportional to the driving voltage or alternatively, driving current, generate
an X-Y trace display having a closed perimeter and whose enclosed area is
proportional to the power delivered per cycle of vibration[8]. The real per cycle power consumption can
then be computed by multiplying the scaled area by the frequency, but
measurement of the energy consumed per cycle is sufficient. Such measurements were made of the
transducer operating alone at free face excursions[9]
(peak-peak displacements) of 50, 75 and 100 microns (for titanium) using a
digital storage oscilloscope and software capable of making area
computations. The excursion was
measured under reflected light with a microscope having a calibrated reticule. Power measurements were taken when the
frequency was adjusted to produce a maximum excursion for a fixed transducer
exciting voltage. Accuracy and
resolution of this measurement was 2.5 microns. The frequency measurements made were accurate to within one
Hertz. The power measurements are
accurate to within ten percent. The
figure illustrates schematically the arrangement of equipment in making the
measurements.
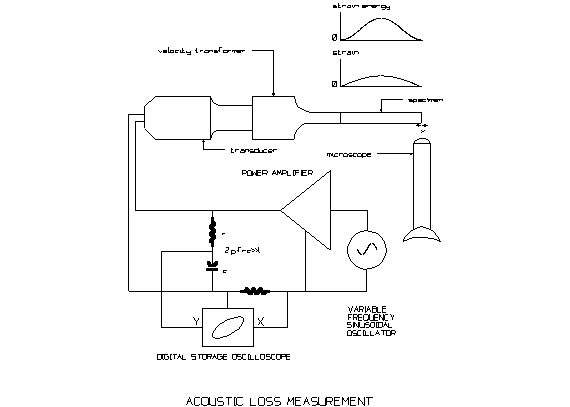
With the specimens attached, the
same measurements were then taken once more. By subtracting the power consumption of the transducer alone taken
at each of the excursions from the consumption with the specimen attached, the
power consumption, P, of the specimen itself was obtained. As it is known that each of the specimens is
undergoing simple half wavelength extensional sinusoidal vibration, the energy
of vibration, E, can be computed as
![]() (1)
(1)
where M is the mass of the
specimen and ![]() , ¦ being the
frequency and e the
excursion of the free face.
, ¦ being the
frequency and e the
excursion of the free face.
The energy consumed by the
specimen per cycle, W, is equal to P/¦ and Q is found as
![]() (2)
(2)
Eq. 1 is only applicable when the elastic loss is independent of strain. In this situation the energy loss per cycle is a constant fraction of the total strain energy of vibration regardless of its distribution within the sample and which is equal to the total kinetic energy. For a slender half wavelength prismatic[10] resonator it is this energy is that given by the expression. If the loss is dependent upon strain, geometrically tailored specimens, such as those used by Mason that subject a well defined region of the resonator to substantially all of and the same strain, can be employed.
Results and
Discussion
The table below presents the findings of these measurements. It is seen that the losses are, over the strain range employed, independent of strain so that the assumption used to obtain Q is justified. But despite the impressive strain/cycle to failure data provided by the manufacturer’s low frequency testing, all of the materials have dynamic elastic losses at ultrasonic frequencies much greater than does annealed titanium. While a Q of 2800 may considered quite high for an electrical tuned circuit, using the data for titanium, a 50 mm (2 in.) round heat treated rod resonant at 20 kHz and operating with an free face excursion of 100 microns, equivalent to a peak strain of 0.12 percent, will consume about 80 watts whereas in the annealed condition the dissipation is likely to be found to be about 10 watts. It is also noted that the Q of Custom 455 had been previously measured at strains below 0.01 percent and found to be in the range of 10,000, in striking disparity with results at elevated strain.
As noted, the Aermet 100 sample fractured cleanly at its center when operation at a cyclic strain of 0.1 percent was attempted. Although both the heat treated titanium and Custom 455 bar survived operating at strains of 0.18 and 0.1 percent respectively, heating at the center of specimen was noted. It is unlikely therefore that either of these materials will rival the performance of annealed titanium in high intensity resonators as elevation in temperature is usually associated with a reduction in fatigue strength.
20 kHz Acoustic
Loss of Heat Treated High Strength alloys
|
sampleD |
Diameter x length mm |
Density kg/m3 |
Young’s Modulus GPa |
cyclic strain percent |
cyclic stress Mpa (kpsi) |
Q |
comments |
|
Custom
455 |
12.6
x 126 |
7750 |
200 |
0.06 |
124
(18) |
1800 |
warm
at center |
|
|
|
|
|
0.09 |
250
(24) |
1800 |
hot
at center |
|
Aermet
100 |
19.3
x 123 |
7789 |
194 |
0.06 |
124
(18) |
5900 |
warm
at center |
|
|
|
|
|
0..09 |
250
(24) |
|
fractured |
|
6Al-4v
Titanium (heat treated) |
9.3
x 127 |
4429 |
110 |
0.06 |
70
(10) |
2800 |
|
|
|
|
|
|
0.09 |
100
(15) |
2800 |
|
|
|
|
|
|
0.12 |
140
(20) |
2700 |
warm
at center |