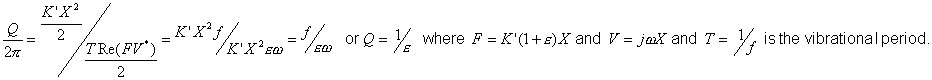A practical
evaluation of harmonic elastic power loss in substantially strained structures
Copyright 1998
David Wuchinich
Modal Mechanics
116 Pinehurst Avenue
New York, NY 10033
Keywords
Ultrasonic, vibration, Q, thermo-elastic, damping, attenuation, dissipation
Abstract
Acute power dissipation accompanying the resonant vibration of ultrasonic tools and surgical instruments can precipitate failure or otherwise limit performance. The Kelvin-Voight first order mathematical model for viscous damping is used to show the power loss in slender elastic structures subject to harmonic strains to be an elementary function of the stress, Young’s modulus, frequency of vibration and the reciprocal of the loss tangent or mechanical Q. The experimental methods that have been used by Balamuth, Mason and other investigators to measure Q and their published results for various materials are reviewed. The expected loss from a typical high intensity ultrasonic surgical tip is computed. A simple method capable of providing rapid qualitative and reliable quantitative Q estimates, is described for use, respectively, in the production process and research laboratory. Values obtained using this method for the Q, modulus and thermo-elastic of selected alloys of interest in the design of high intensity resonators are provided.
Introduction
The development of high intensity ultrasonic resonant vibrators for use in cutting and aspirating tissue in surgical procedures has significantly broadened application for this technology[1][2][3] that had been principally confined to dental prophylaxis and cataract excision and to the industrial technology of ultrasonic welding. To provide the requisite ultrasonic motion of the surgical tip portions of the horns providing this motion are subjected to continuous cyclic strains in the range of 0.2 percent. Heating produced by internal friction within the horn material can limit its ability to survive such exposure. Cooling is frequently employed to maintain a physiologically compatible tip temperature as well as to reduce tip failure caused by the well documented diminution of the yield stress produced by temperature elevation[4]. Computation of expected losses at specified performance levels is therefore of interest in design if such methods can anticipate overheating, excessive power demands upon the transducer or the likelihood of material failure. Accurate estimation of power loss is also important in the design of corpulent industrial horns where the sheer bulk of the horn material may severly limit the effectiveness of surface cooling in removing heat and therefore mandate a reduced operating level.
The first part of this paper reviews the elementary theory and published data. The second section describes a simple technique for making measurements of elastic losses on sample lots of stock material prior to fabrication.
PART 1
Analysis
Mason has comprehensively reviewed the phenomenological representations of irreversible energy loss in strained solids and models based upon the classical concept of viscoelasticity introduced by Maxwell, among others[5]. For present purposes, where an estimate of the power dissipation density is desired in resonant vibration when at least a part of the structure is subjected to large cyclic strains, the elastic modulus, Y, can be represented as a complex number: Y=E(1+je). This representation is readily apparent from the force equation for a single degree of freedom system containing the discrete elements of mass M, spring constant K and viscous damping factor z, all of which are identified in Figure 1
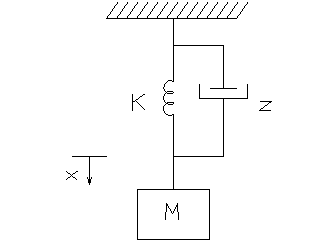
Figure 1 – Simple harmonic resonator with visco-elastic damping
![]()
For time harmonic motion the viscous damping factor, z, can be embedded in a complex spring constant, K, for time harmonic motion:
![]() ,
,
where K’ is the “static” value of the spring constant
The equation of motion then becomes, for ![]()
![]()
showing that eK’
can be considered an equivalent representation of z. However, by stipulating that the damping be proportional to the
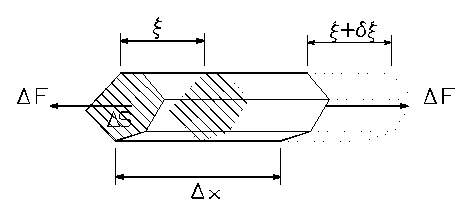
spring constant, instead of being a separate quantity, the system Q, defined as
the ratio of the energy stored to that lost per cycle multiplied by 2p, can
easily be shown to become, rather than the familiar expression wM/z,
just simply 1/e. Making the viscoelastic loss proportional to
the modulus implies that the energy loss per cycle is proportional to the
cyclic energy of vibration at any time with the consequence that their ratio is
independent of the vibrational frequency[DW1].
For systems having distributed mass, elasticity and damping, the average power loss in a slender fiber element (Figure 2) executing harmonic motion at a frequency f can be written as
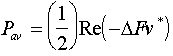 (1)
(1)
|
Figure 2 - Elastic fiber element |
where DF is the force acting on the element over the surface S and
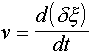 is the velocity of the
element extension, dx
is the velocity of the
element extension, dx
where
![]() ,
, ![]() ,
, ![]() . *
denotes the complex conjugate.
. *
denotes the complex conjugate.
From Hook’s Law, the stress DF/DS is then
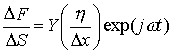
where Y is Young’s modulus.
Using these expressions, Eq. 3 becomes
![]() (2)
(2)
If Y is real,
there is no power loss as the product is imaginary. But if ![]()
where e represents internal friction and E’ can be considered the static value of Young’s modulus, then
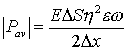 . (3)
. (3)
As the stress, s
= DF/DS, in
the bar is related to h
as ![]()
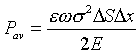
and the average power loss per unit volume of material, p, is
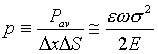 .
.
As discussed, e can be replaced by the reciprocal of the quality factor, Q. Using this relation, the volumetric loss density becomes
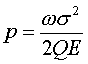 . (4)
. (4)
In the situation of a general harmonic displacement resulting from resonant vibration, integration of the square of the mean stress over the volume and knowledge of the mechanical Q, which has been or can be measured separately for materials, permits the average power consumption to be computed from knowledge of the modal frequency and Young’s modulus. Note that even for values of Q>10, the inequalities permitting the simplification shown by Eq. 4 are satisfied.
As this analysis considers only stress and strain in one direction, it is limited to slender bars (beams), but it may also be used in situations where displacements in all three directions are the same, as for example in a radially oscillating sphere or shell or thin ring, if E is replaced by the bulk modulus, K:
![]()
where n is Poisson’s constant[6]. Extension of the computation to other structures of practical interest where displacements in two or three dimensions must all be separately considered is today properly the subject of finite element analytical techniques. To the author’s knowledge none of the commercial stress analysis programs in common use offer as yet the ability to compute strain energy per element, although the information to perform the computation is readily available from the displacements computed by these programs. Numerical methods also offer the potential for computing thermal gradients once the cyclic energy loss per element is known.
Q may be computed from attenuation measurements of acoustic wave propagation by using the relation
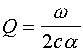
where c is the sound velocity and a is the attenuation in nepers per unit length[7]. However, other techniques have been described employing the actual resonant vibration of samples.7 5 [8]. Reported findings are tabulated in Figure 3 below.
Figure 3
Measured room
temperature Quality factors for selected materials
|
Material |
Q |
Notes |
|
90Ti-6Al-4V Titanium alloy[9] |
20,000 |
Annealed. Strain < 0.003, 17 kHz |
|
Low carbon steel[10] |
250 |
Annealed, Strain
<0.0001, 23 kHz |
|
Lead[11] |
500 |
Commercially pure,Strain
< 0.00025 |
|
Aluminum11 |
10,000 |
|
|
Magnesium11 |
5700 |
|
|
Tungsten carbide steel11 |
8180 |
|
|
Bakelite5 |
200 |
Strain < .0024,
17.6 kHz |
|
Polycarbonate
(unreinforced)[12] |
100 |
Strain 0.005, 20kHz |
|
Unfilled polypropylene12 |
100 |
Strain 0.005, 20 kHz |
Investigators have shown that, for many materials including plastics and metals, below a threshold value, Q is largely independent of the harmonic frequency and strain.5 [13].
For purposes of historical reference a reproduction of Mason’s original test apparatus employed in 1958 to measure the Q of various materials, including bakelite, is shown in Figure 4. Mason was one of the first investigators to use barium titinate transducers to explore and develop the then nascent field of high intensity, low frequency ultrasonics and his seminal work, along with that of Lewis Balamuth, L.D. Rosenberg, E.A. Neppiras, Y. Kikuchi and R. Pohlman has been of enormous benefit to those engaged in high intensity ultrasonic development.

Figure 4
Dissipation due to cyclic losses can be significant in the operation of high intensity ultrasonic resonators used in plastic welding equipment and in ultrasonic surgical instruments Although the expressions for volumetric cyclic power dissipation developed here are only applicable to slender structures, many ultrasonic tools approximately comply with this restriction.[14] Consider the elementary example of a slender rod undergoing half wavelength extensional vibration, as shown in Figure 3.
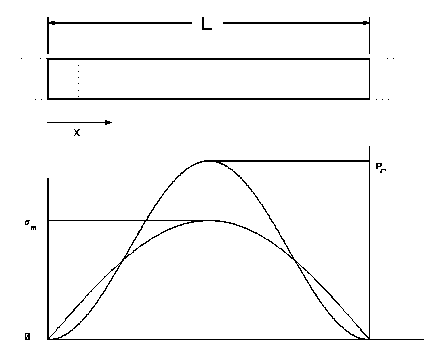
Figure 5
Extensional resonant displacement, stress sM and relative elastic power loss density p in a slender rod.
In this case the stress can be shown to be[15]
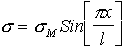
The power density is then
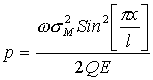 .
.
Integrating over the volume of material
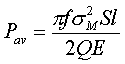
where S is the cross sectional
area. As ![]() for the first
extensional half wavelength (l)
resonance and lf = c, the extensional sound velocity,
for the first
extensional half wavelength (l)
resonance and lf = c, the extensional sound velocity,
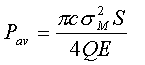 (half wave length
extensional resonator)
(half wave length
extensional resonator)
For 6Al-4V Titanium, a material commonly employed in such resonators, sM = 40 Kpsi (276 Mpa), E = 16 Mpsi (110 GPa), c @ 200 K in/s (5 Km/s) and Q @ 20,000, it is found that for a bar 0.25 inch (6.35 mm) in diameter Pav ~ 40 in lbs/s @ 4 Watts. Clearly, even in very slender rods that are subject to large dynamic stress, such as those used for microsurgical procedures, unavoidable elastic power loss is significant and cooling may be required.
It is important to note that, while for the same dynamic stress Pav remains the same per unit wavelength, the power density, p, (and hence thermal threat) increases in direct proportion to frequency. A 60 kHz half or quarter wavelength bar will exhibit, for example, 3 times the elastic energy loss per unit volume of one operating at 20 kHz subject to the same cyclic stress. If the loss is significant at one frequency it likely to be intolerable when the frequency is doubled, even when the vibration amplitude is properly halved to maintain the same cyclic stress.
Figure 6 illustrates a similar computation for a high intensity 23 kHz extensional resonator[16] with which the author is familiar and which is used to perform ultrasonic surgical aspiration of neurologic neoplasms. The stress distribution for this device was computed by direct integration of the wave equation under the assumption that motion everywhere is substantially extensional. The slender portion, or tip, is made of 6Al-4V titanium and operated at a maximum cyclic stress of 40,000 (276 Mpa) psi. The tip is designed to subject a substantial portion of its length to this stress so as provide as much extension at the free end as possible. Computation reveals that the total power consumed by the tip is approximately 1.5 W, but as the actual volume of material is only slightly more than 0.5 cm3, it is clear that without cooling (which is provided by irrigating fluid) the metal will become warm and its operating life curtailed.
Figure 6 also shows that in regions of structures vibrating in the 20 kHz range experiencing dynamic stress of 40,000 psi (276 Mpa), a power loss of between 50 and 60 watts per cubic inch can be expected in annealed Titanium. While this loss can be tolerated in high intensity slender, pencil thin resonators, in industrial bar horns or stepped bar horns, this level of stress is equivalent to a output free face deflection of about 3.5 mils (7 mil stroke). Thermal conductivity precludes use of thick solid horns operating at this level in continuous service applications - even when surface cooling is provided. For process applications, such as laminating and non-woven bonding, either the horn thickness or the stress must be reduced if temperature elevation due to elastic loss, and concomitant horn failure, is to be avoided. In fact, the maximum output free face deflection used in such applications is about 2 mils (4 mil stroke) (50 microns amplitude, 100 micron stroke), corresponding to a dynamic stress at 20 kHz of about 20,000 psi (138 Mpa) and even at this level air cooling of the horns may be required to provide acceptable service life.
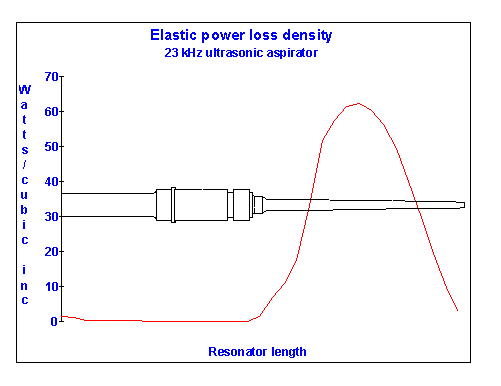
Figure 6
Elastic power loss density distribution of an ultrasonic surgical aspirator
Part 2
Q by Chiming
Although investigators have computed the mechanical Q of materials from attenuation, phase measurements or by the difference between the electrical power consumed by a resonant transducer exciting a test resonator and that drawn when operating alone at the same vibration amplitude and frequency5 9 12, an extremely simple method is available for materials whose Q exceeds approximately 1,000. As the examples just discussed show, to avoid excessive elastic power loss in resonators subjected to large dynamic stress this limitation does not practically restrict the regime of interest.
Remembering that the Q is defined as 2p times the ratio of total vibrational energy to the energy lost per cycle and that vibration energy is proportional to the square of the amplitude, it can be shown, since the rate at which energy is lost per cycle is proportional to the total energy of vibration at any time, that the amplitude, x, at any point on a resonator initially excited into resonant vibration, and then allowed to freely decay, must diminish exponentially:
![]() (5)
(5)
where f is the frequency, t is the time of the observation and xo is the initial amplitude.
If amplitudes x1 and x2 are measured at times t1 and t2, from Eq. 5 ,
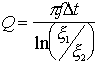 (6)
(6)
where t1 - t2 = Dt
A specimen in the form of the common wind chime or xylophone resonator offers an acceptable example for such measurement. The test arrangement is sketched in Figure 7. The same principle has been used by in at least one other investigation to measure the elastic loss and wave dispersion in an aluminium alloy at various frequencies[17].
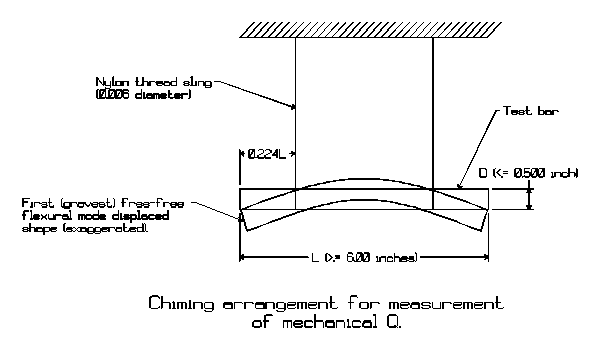
Figure 7
The chime can easily be made to vibrate in the first free-free flexural resonant mode if suspended at the motional nodal locations identified in the figure. As a typical example, a stainless steel bar 0.5 inches (12.7 mm) in diameter and 6.0 inches (152 mm) in length will resonate, when struck with a cork or hard rubber faced hammer at its ends or center, with a clear plainly audible fundamental tone of about 2500 Hz, a frequency which also happens to elicit the most sensitive response of the human ear.
A sound meter placed near the center of the bar and connected to a storage oscilloscope and frequency counter can be used to provide quantitative measurements. One such oscillogram obtained for a sample of the machineable ceramic, MACORTM[18] is shown in Figure 8. With knowledge of the frequency, and by measuring the peak-peak amplitude at two distinct times, the Q can be quickly computed. The slight modulation evident in the decay envelope frequently occurs in testing and may be attributable to slight asymmetry in the bar cross section. Under such circumstances the bar can vibrate simultaneously in two planes, each having a frequency only slightly different from the other. The result produces a familiar beat frequency. The Q can be determined in the presence of modulation by taking signal values at successive maxima or minimina. If desired, it is usually possible to remove beating by incremental rotation of the bar between strikes until a position is obtained where vibration takes place only in one plane and uniform monotonic decay results.
Figure 10 tabulates typical measurements made on samples having the dimensions of Figure 7 of a variety of materials in various identified conditions. The value obtained for annealed 6Al-4V titanium agrees well with that shown in Figure 3. Successive measurements on the same waveform reveal a repeatability within 10 percent.
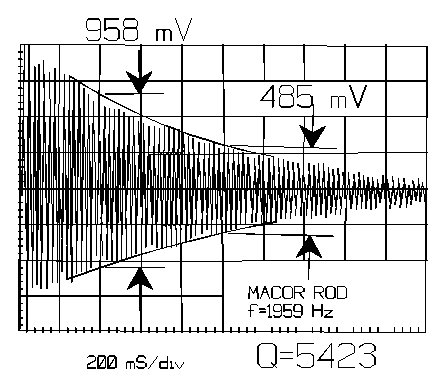
Figure 8
Decay envelope
for a ceramic chime
Use of slings having a modulus of elasticity and diameter small compared to that of the specimen assures that the damping introduced by the supports is negligible. For the tests reported here, nylon slings 0.006 inch (150 microns) in diameter were employed. Measurements made of MACORä levitated by ferrite magnets in combination with an air bearing have produced substantially the same result as given in Figure 8. A schematic representation of the levitation apparatus is shown in Figure 9.
Losses produced by radiation into the surrounding air were also evaluated on test samples having diameters in the range of 10 mm and a Q in the range 20,000 to 50,000 by performing the measurements in a partial vacuum of 380 mmHg. The measured values at reduced pressure remained unchanged from the atmospheric results, although an effect upon material having a Q of 250,000 has been reported in a study where measurements were made at a pressure of 35 microns17.
Viscous losses produced by vibration of the chimes in air were studied by making measurements of a bar having a nominal atmospheric Q of 50,000 and repeating the measurements in an atmosphere of propane at room temperature and at a pressure of 485 mmHg. The pressure was reduced to equalize any radiation loss due to the difference in density between air and the gas20, although radiation loss for this value of Q appears to be neglible. It is not expected that this reduction in pressure will affect the measurement as Crookes’ classic investigation[19], confirming Maxwell’s, Kundt’s and Warburg’s work, showed that the viscosity of gases does not appreciably change until pressures are lowered to micron levels. As the viscosity of propane is less than half that of air[20], the negative result obtained from this comparison appears to render the affect of such losses beyond concern for values in the range examined here.
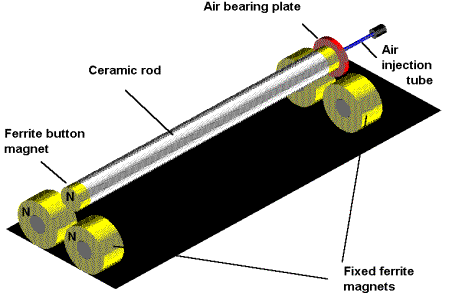
Figure 9
Magnetically levitated test chime
|
Material |
Condition |
Q |
|
6Al-4V Titanium |
Lots, as received |
2,000-6,000 |
|
6Al-4V |
Annealed |
18,000-22,000 |
|
17-4PH Stainless Steel |
Annealed |
7,000 |
|
PH15-7Mo Stainless Steel |
Annealed |
17,000 |
|
PH15-7Mo |
Hardened |
17,000 |
|
PH13-8Mo Stainless Steel |
Annealed |
10,000 |
|
Custom 455 Stainless Steel |
H900 condition |
10,000 |
|
MACORTM |
As received |
5,000 |
Figure 10
Chiming Q of
Various Materials
The technique is also capable of producing rapid qualitative information to the trained ear where only large disparities in loss need detection. By lightly holding a specimen near the ear between two fingers at its upper most node and striking the lower end with a wooden or plastic rod, both of which are unlikely to elicit the production of prolonged overtones, inspectors can be trained to quickly assess by the “ring down time” if the material is likely to fail or excessively heat in use.
Finally, it is, of course, also possible to determine the extensional sound velocity, c, if the specimen is a prismatic bar, as15
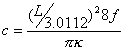
where L is the bar length, f the frequency and k the radius of gyration of the bar cross section about the neutral strain axis in bending.
Resonator design based upon velocities computed in such a manner have shown the values to be accurate, but often disconcertingly different from those given by mills, in standard handbooks or computed from listed typical values of Young’s Modulus and material density. The author has found that the densities provided for alloys are usually accurate. Variations between tabulated and measured sound velocities are therefore entirely attributable to differences in the elastic moduli.
All of the analyses presented in this report assumes that the mechanical strain is principally in one direction and that the rotary inertia of bending can be neglected. Rayleigh[21] has shown that this condition is satisfied for this geometry if the square of the bar’s length is much greater than the square of its diameter. The chime dimensioned in Figure 7 satisfies this requirement.